23년 인천영재학고 2차 기출문제풀이 22년7월10일시행

인천,대전,대구,세종,광주는 공동출제로 비슷한 문제가 많습니다.

1번 문제 (인천, 대전, 대구 공동출제)

1. 한 변의 길이가 20인 정삼각형 한 개를 남는 부분 없이 여러 개의 정삼각형으로 나누려고 한다. 예를 들어 그림과 같이 한 변의 길이가 20인 정삼각형 한 개를 한 변의 길이가 15인 정삼각형 1 개와 한 변의 길이가 5인 정삼각형 7개로 나눌 수 있다.

다음 물음에 답하시오.

(1) 한 변의 길이가 5인 정삼각형으로만 나누려고 할 때, 나누어진 정삼각형의 개수를 구하시오.

(2) 한 변의 길이가 1,4,15인 정삼각형으로 나누려고 한다. 나누어진 정삼각형의 최소 개수를 구하고, 그 이유를 설명하시오. (단, 제시된 세 가지 종류의 정삼각형을 모두 사용하지 않아도 된다.)

(3) 한 변의 길이가 자연수인 5개 이상의 정삼각형으로 나누려고 할 때, 가장 적은 개수의 정삼각형으로 나눌 수 있는 방법을 설명하시오. (단, 여러 종류의 정삼각형을 사용할 수 있다.)

1번 문제 해설

(1) 16개

(2) 넓이의 관점에서 가능한 경우를 찾아보자
x+16y+225z=400에서 z=0 일때 y=25개 가능
z =1 일때 x+16y=225에서 y=10,z=15에서 26개 이상 따라서 최소는 25개

(3) 우선 세 꼭지점을 각각 포함하는 정삼각형이 있어야 한다. 그리고 세 변도 포함해야 한다.
세 구석을 채우고 나면 사다리꼴의 모양을 정삼각형3개로 채울수 있는데 이때는 변의 길이가 자연수 아니다. 불가능

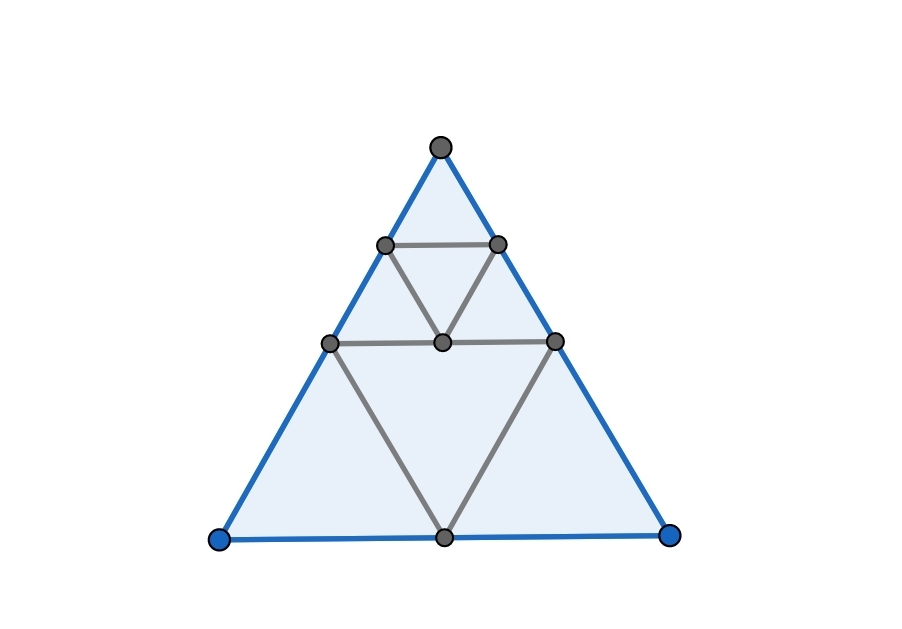
다음 그림은 변의 길이 10,5인 정삼각형 7개로 만든 삼각형이다.

2번 문제 (인천, 세종, 대구, 광주 공동출제)

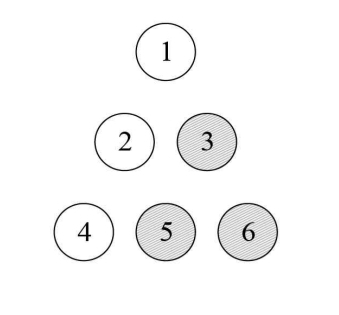
2. 그림과 같이 1에서 6까지의 숫자가 적힌 6개의 전구와 A, B, C, D 4개의 버튼이 있는 장치가 있다

다음은 버튼과 전구의 연결 관계를 나타낸 표이다. 버튼을 누르면 연결된 전구 중 켜진 전구는 꺼지고, 꺼진 전구는 켜진다.

예를 들어, 버튼 A를 누르면 전구 1, 전구 2, 전구 3 중 켜진 전구는 꺼지고, 꺼진 전구는 켜지며 전구 4, 전구 5, 전구 6 은 변화가 없다. 다음물음에 답하시오. (단, 2개 이상의 버튼을 동시에 누르지 않는다)

(1) 모든 전구가 꺼진 상태에서 버튼 A, B, C, D를 한 번씩 눌렀을 때, 켜져 있는 전구를 빗금으로 색칠하시오.

(2) 그림과 같이 전구 3, 전구 5, 전구 6이 켜져 있을 때 모든 전구를 켜고자 한다. 버튼을 누르는 최소 횟수를 구하고, 그 이유를 설명하시오.

(3) 이 장치에 전원을 연결하면 각 전구가 임의로 켜지거나 꺼져있는 상태인 '처음 상태'가 주어진다. '처음 상태'에서 버튼을 눌러 모든 전구를 켜려고 한다. 장치에 전원을 연결했을 때, 모든 전구를 켜는 것이 가능한 '처음 상태'가 주어질 확률을 구하고, 그 이유를 설명하시오. (단, 버튼은 여러 번 누를 수 있다.)

2번 문제 해설

(1) 모든 전구를 색칠하면 된다.

(2) 1,2,4 번전구는 꺼져 있으므로 전구에 연결된 버튼을 홀수번 눌러야 하고 3,5,6번 전구는 켜져 있으므로 전구에 연결된 버튼을 짝수번 눌러야 한다. 1번 전구는 버튼 A와, 4번 전구는 버튼 B와, 6번 전구는 버튼 C로만 연결되어 있다는 것이 핵심이다.

최소 버튼 A, B는 한번 눌러야 1,4번 전구를 킬 수 있다. D를 한 번만 더 누르면 모든 전구를 켤 수 있으므로 최소의 횟수는 3이다.

(3) 1,4,6번 전구는 버튼 A, B, C에만 연결되어 있으므로 1,4,6번 전구를 먼저 생각한다면 1,4,6번 전구의 상태와 관계없이 전구를 모두 킬 수 있다. 1,4,6번 전구를 켜기 위해 A, B, C 버튼을 누른 이후에 버튼 D로만 전구 2,3,5번을 켤 수 있는 확률을 구하는 문제와 같아진다.

D버튼에는 2,3,5번이 모두 연결 되어 있으므로 2번을 켜기 위해 버튼을 누른 이후 3번 5번 전구까지 켜져 있을 확률은 1/4이다.

3번 문제 (인천, 세종, 대전 공동출제)